1.해쉬테이블
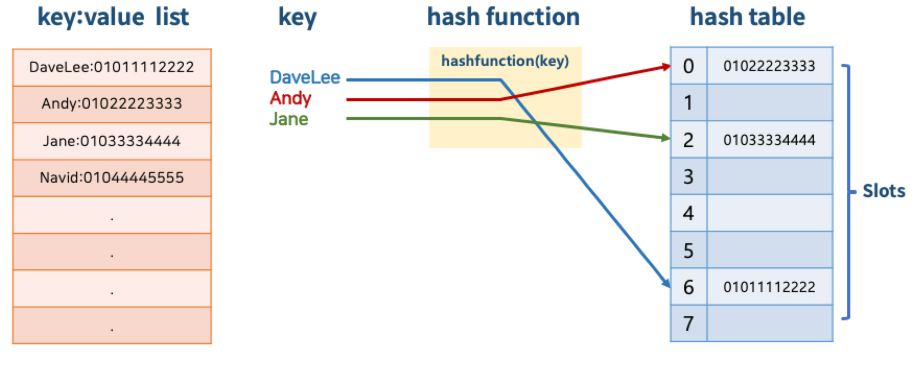
1.2.개념
- 해쉬 함수(Hash Function)을 통해 키(Key)에 데이터(Value)를 매핑할 수 있는 데이터 구조.
- 키를 통해 데이터가 저장되어 있는 주소를 알 수 있으므로, 저장 및 탐색속도가 빠름.
1.3.장/단점 및 주요용도
| 장점 | 단점 | 주요용도 |
| ●데이터 저장/읽기 속도가 빠르다(검색 속도가 빠르다) ●키에 대한 데이터가 있는지(중복)확인이 쉽다. |
●저장공간이 많이 필요하다. ●충돌발생 가능성이 있다. 별도 자료구조가 필요하다. |
●검색이 많이 필요한 경우 ●저장, 삭제, 읽기가 빈번한 경우 ●캐쉬 구현시(중복확인이 쉽다) |
2.트리

2.1.개념
- Node와 Branch를 이용해서 순회를 막는 데이터 구조
- 이진 트리(Binary Tree) 형태의 구조로 탐색(검색) 알고리즘 구현을 위해 많이 사용함.
2.2. 용어
- Node: 트리에서 데이터를 저장하는 기본 요소 (데이터와 다른 연결된 노드에 대한 Branch 정보 포함)
- Root Node: 트리 맨 위에 있는 노드
- Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
- Parent Node: 어떤 노드의 다음 레벨에 연결된 노드
- Child Node: 어떤 노드의 상위 레벨에 연결된 노드
- Leaf Node (Terminal Node): Child Node가 하나도 없는 노드
- Sibling (Brother Node): 동일한 Parent Node를 가진 노드
- Depth: 트리에서 Node가 가질 수 있는 최대 Level
2.3.1.이진트리와 이진 탐색 트리(Binary Search Tree)
- 이진 트리: 노드의 최대 Branch가 2인 트리
- 이진 탐색 트리(Binary Search Tree. BST): 이진트리 개념에 더해 왼쪽 노드는 해당 노드보다 작은 값, 오른쪽 노드는 해당 노드보다 큰 값을 배치하는 조건을 가지고 있음

2.3.2. 이진트리와 정렬된 배열간의 탐색 비교
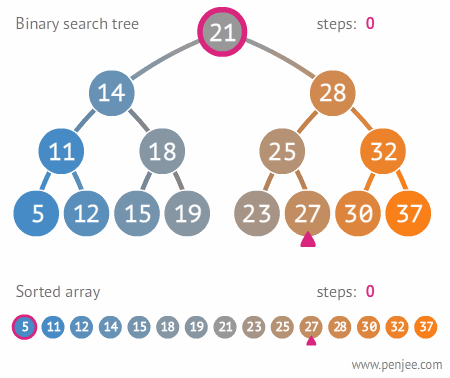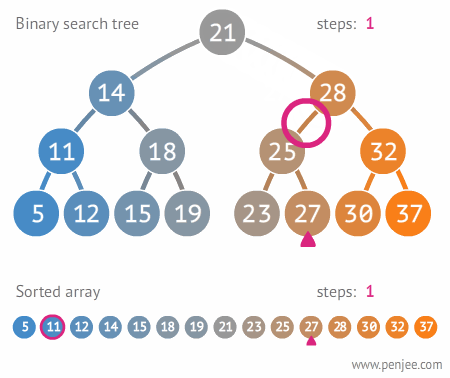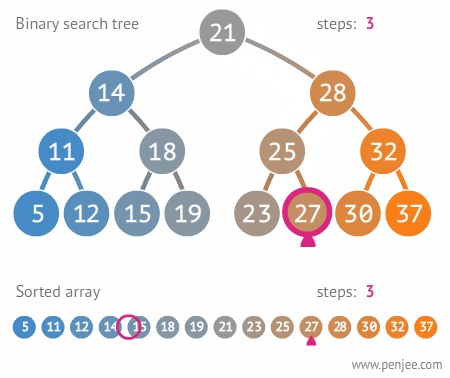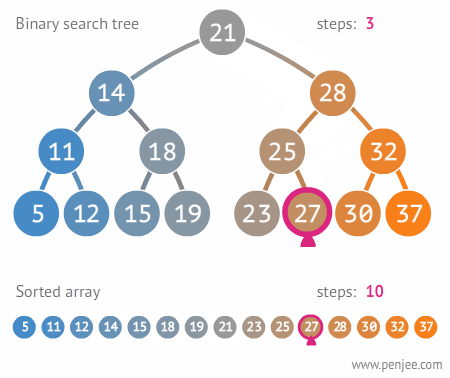
2.3.3 이진 탐색 트리의 삭제
Case1. Leaf Node 삭제
- 삭제할 Node의 Parent Node가 삭제할 Node를 가리키지 않도록 한다.

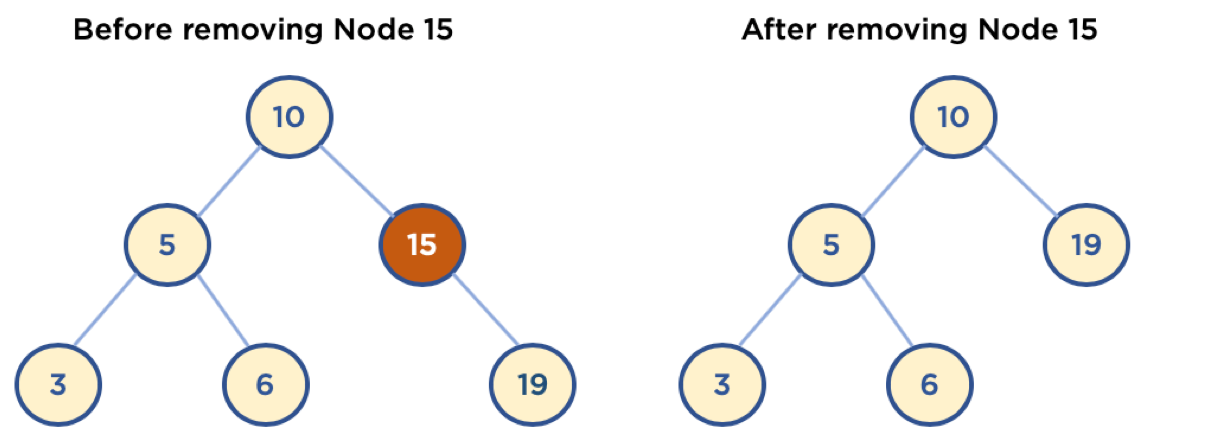
Case2.Child Node가 하나인 Node삭제
- 삭제할 Node의 Parent Node가 삭제할 Node의 Child Node를 가리키도록 한다.
Case3.Child Node가 두 개인 Node 삭제
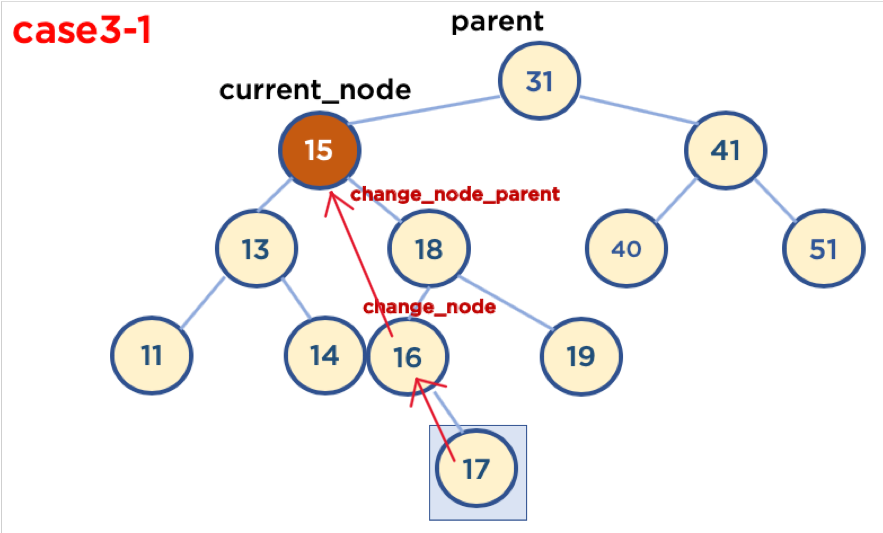
Case3-1.삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
Case3-1-1.삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
Case3-1-2.삭제할 Node가 Parent Node의 왼쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때 -> 가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문임
Case3-2.삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록 한다.
Case3-2-1.삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 Child Node가 없을 때
Case3-2-2.삭제할 Node가 Parent Node의 오른쪽에 있고, 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 가진 Node의 오른쪽에 Child Node가 있을 때 ->가장 작은 값을 가진 Node의 Child Node가 왼쪽에 있을 경우는 없음, 왜냐하면 왼쪽 Node가 있다는 것은 해당 Node보다 더 작은 값을 가진 Node가 있다는 뜻이기 때문

2.3.4. 이진 탐색 트리의 장점과 주요용도
| 장점 | 단점 | 주요용도 |
| 탐색 속도가 빠름 | 링크드 리스트와 동일한 성능을 보여줄 수 있다. | 데이터 검색(탐색) |
3.힙
3.1.개념
●데이터에서 최대값과 최소값을 빠르게 찾기 위해 만들어진 완전 이진 트리(Complete Binary Tree)
*완전 이진 트리:노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
3.2.힙(Heap)구조
●최대값을 구하기 위한 구조(최대 힙, Max Heap)과 최소값을 구하기 위한 구조 (최소 힙, Min Heap)으로 분류 가능
●힙의 조건
①각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같다.(최대 힙인 경우), 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 작다.
②완전 이진 트리 형태를 가진다.
●힙과 이진 탐색 트리의 공통점과 차이점
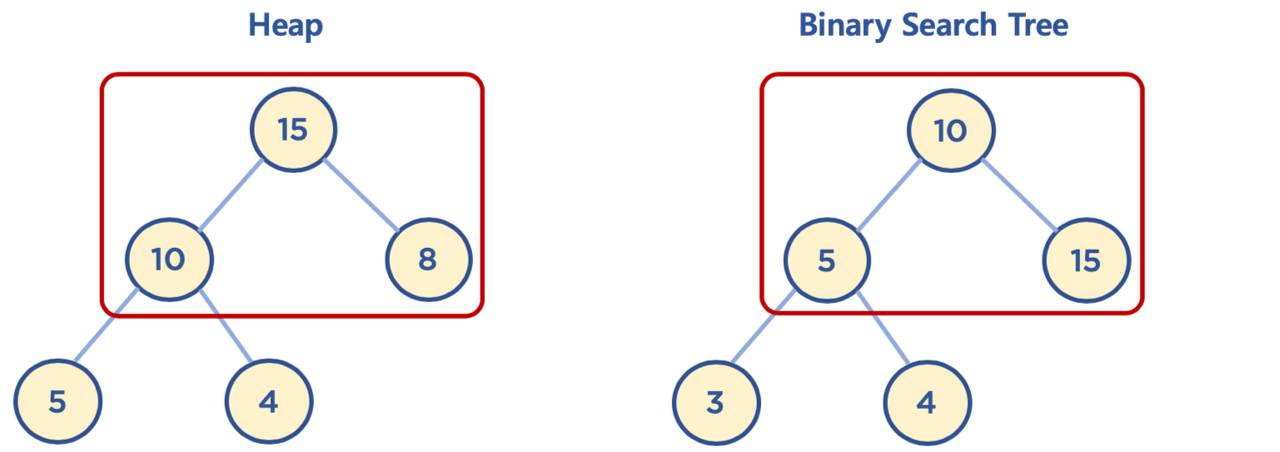
| 공통점 | 차이점 |
| 모두 이진 트리 | 힙: 각 노드의 값이 자식 노드보다 크거나 같다(Max Heap), 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽에 배치한다는 조거닝 없다. 이진 탐색 트리는 탐색을 위한 구조, 힙은 최대/최소값 검색을 위한 구조 |
3.3.힙(Heap) 동작
3.3.1.삽입하기
①기본동작
:왼쪽 최하단부 노드부터 채워지는 형태
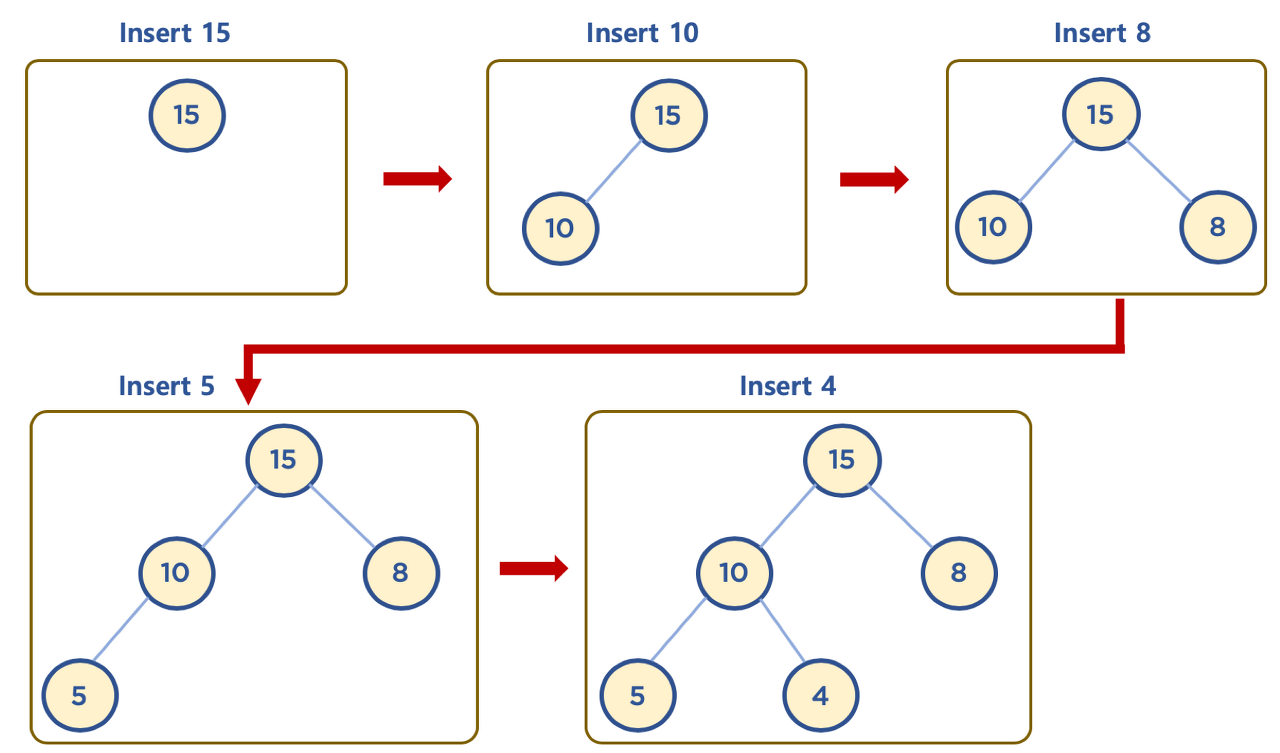
②삽입할 데이터가 힙의 데이터보다 클 경우(Max Heap)
:채워진 노드 위치에서 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복한다.

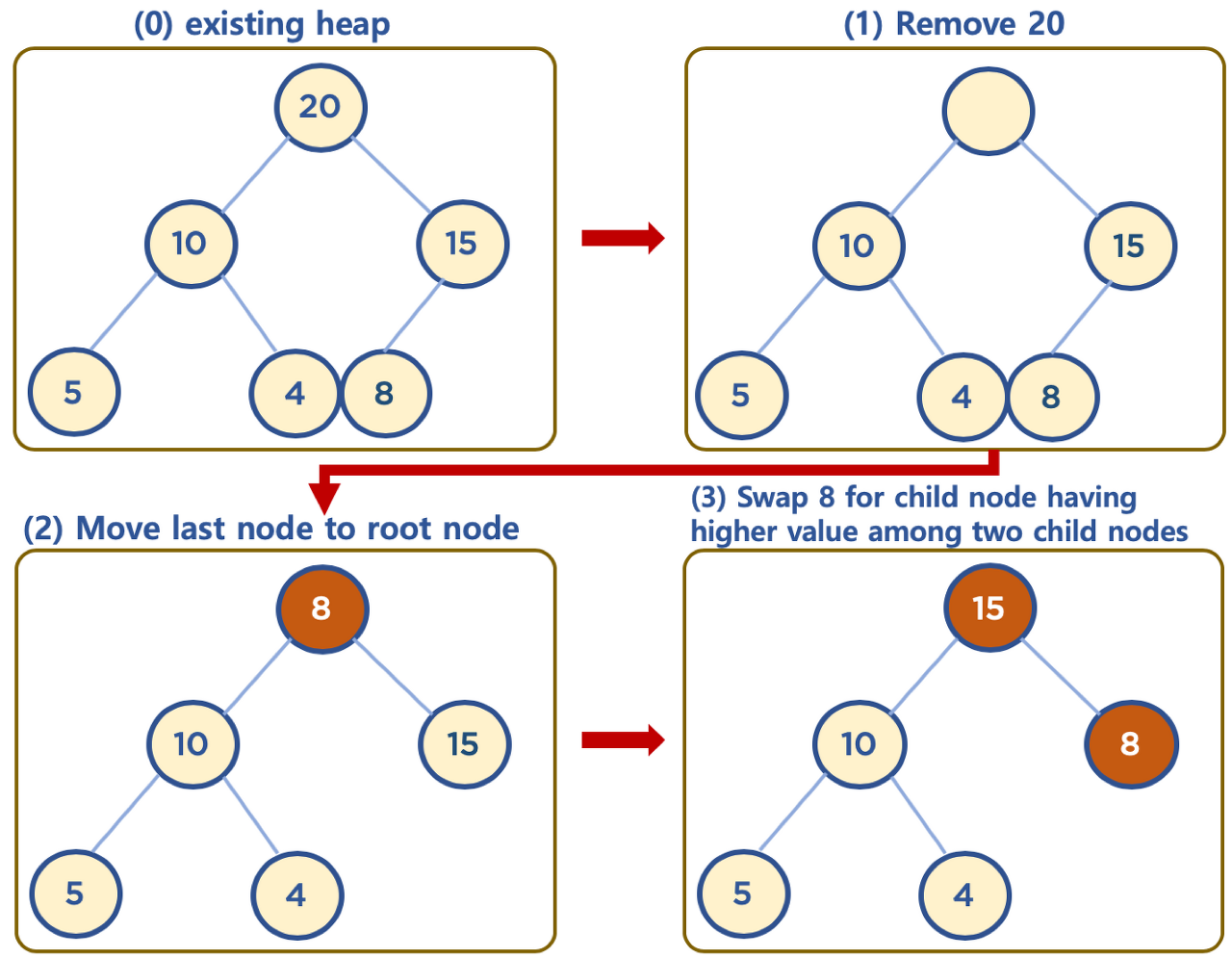
3.3.2. 삭제하기
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최대값 또는 최소값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
- root 노드의 값이 child node 보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
3.4.힙(Heap) 구현
3.4.1 힙과 배열

- 부모 노드 인덱스 번호 (parent node's index) = 자식 노드 인덱스 번호 (child node's index) / 2
- JAVA 에서는 / 연산자로 몫 을 구할 수 있음
- 왼쪽 자식 노드 인덱스 번호 (left child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2 + 1
참조
- 패스트캠퍼스 / 한 번에 끝내는 코딩테스트 369 Java편 초격차 패키지 Online.
'CS > 자료구조와 알고리즘' 카테고리의 다른 글
| [CS/자료구조와 알고리즘] 알고리즘 개념 (0) | 2023.03.10 |
|---|
